論理演算子「AND」「OR」「NOT」「NAND」「NOR」の違いについて
プログラミングなどで使う論理演算子ですが、名前だけ見ているとどれがどれだか分からなくなることありませんか?
ということでベン図を使って簡単にまとめてみました。
ベン図
論理演算子の解説をする前に、解説に使う「ベン図」について簡単にご説明します。
(ベン図が問題なくわかる方は論理演算子まで飛んでください)
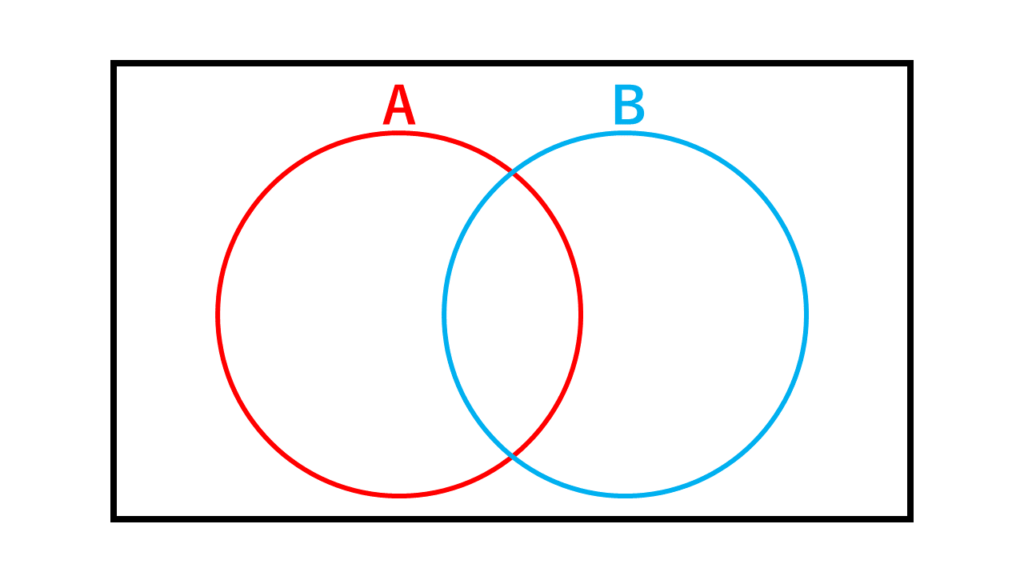
ベン図とは上の図のことを言います。
本来の使い方は中学校くらいで習う集合を表すのに使います。
「A」という条件を満たすものは赤い丸の中、満たさないものは外に入ります。
同様に「B」という条件を満たすものは青い丸の中、満たさないものは外に入ります。
「A」と「B」という条件両方を満たす場合は、2つの丸が交わっている場所に入ります。
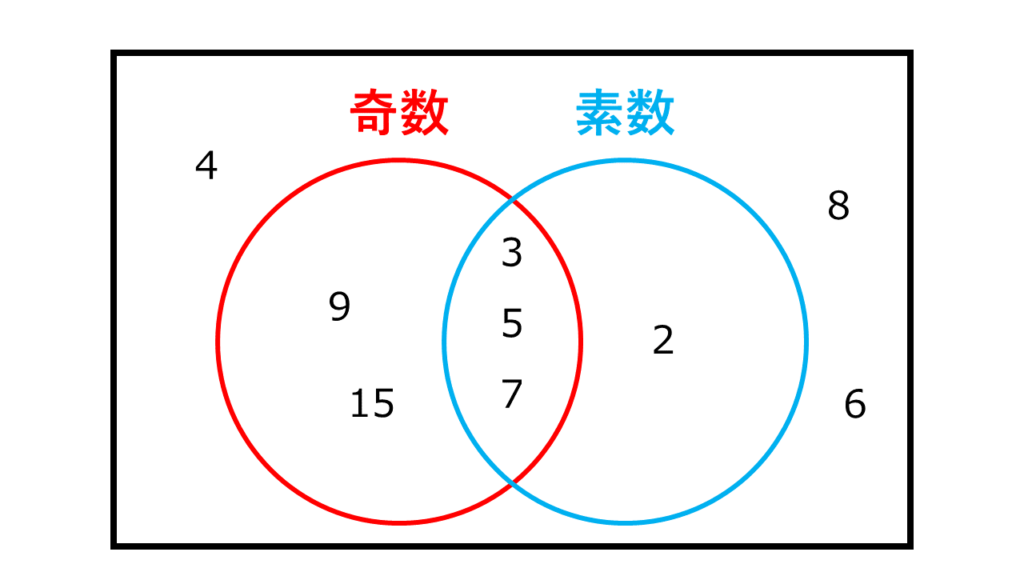
例えば奇数と素数を条件にした場合は上の図のようになります。
このベン図は集合を表す以外にも、今回解説するような論理演算に対しても同じような意味合いで使用します。
論理演算子
論理演算関係の基本、論理演算子について解説します。
論理演算子はプログラミングや命題などで用いられます。
論理演算子は「AND」「OR」「NOT」の論理演算の基本的な3つがあります。
ちなみに今回は条件が2つの場合について解説しますが、3つ以上の場合も同様の意味になります。
AND
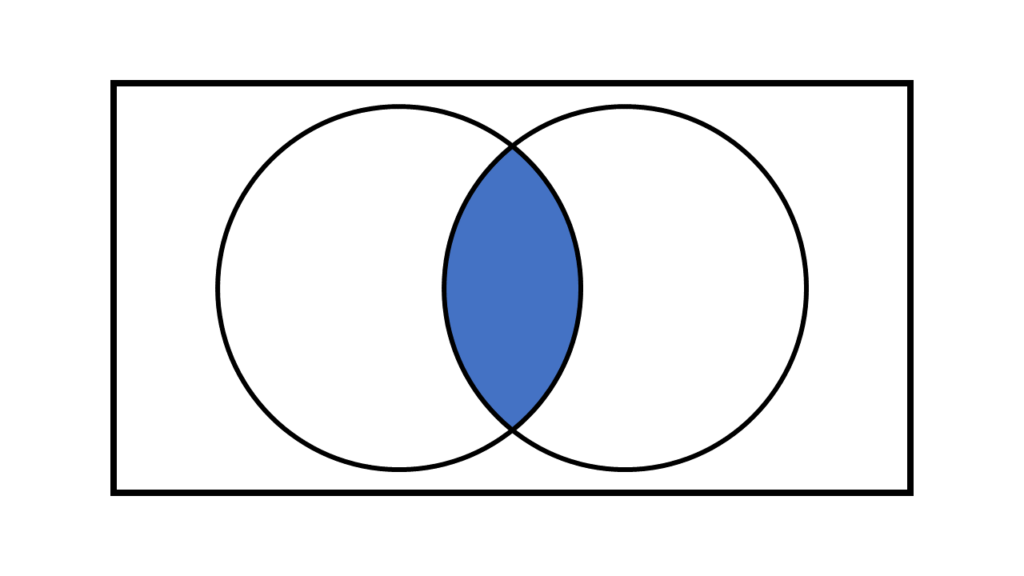
ANDは2つの条件両方を満たすものが真となります。
ですので上の図のように2つが重なった部分のみが対象になります。
OR
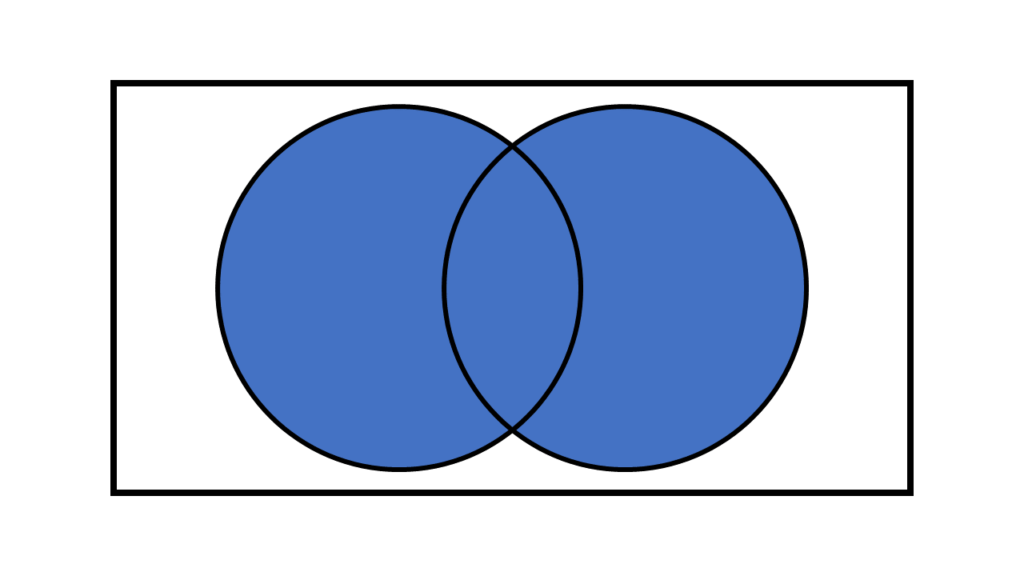
ORは2つの条件のいずれかを満たすものが真となります。
どちらか一方の条件を満たすものはもちろん、両方の条件を満たすものも真です。
NOT
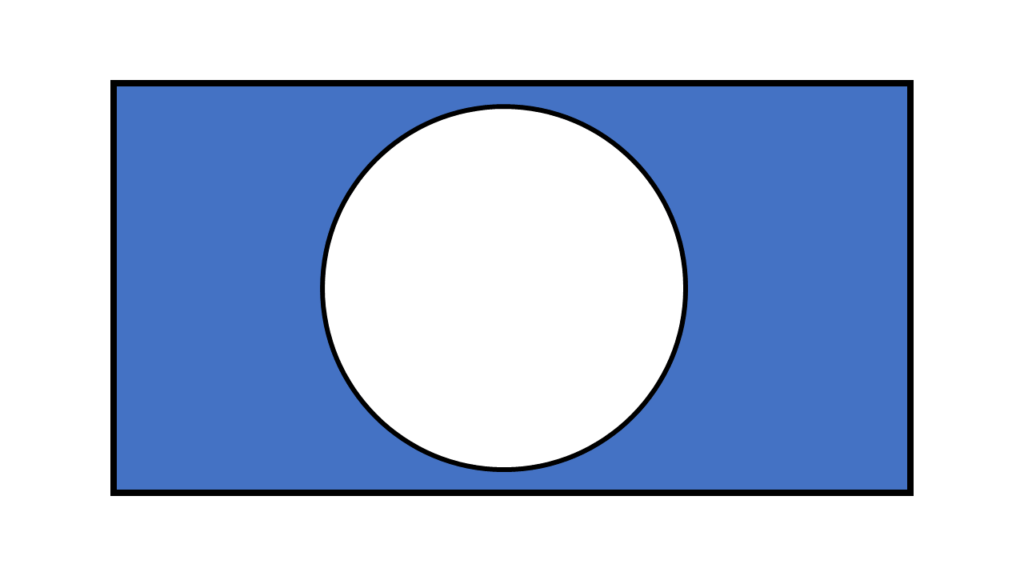
NOTはその条件を満たさないものを真とします。
これだけは複数の条件を比較するのではなく、1つの条件に対する論理演算子です。
否定論理和・積
先ほどの論理演算子「AND」「OR」に「NOT」を組み合わせて使うことがあります。
これらをそれぞれ「否定論理和 (NOR)」「否定論理積 (NOAND)」と呼びます。
この2つの特徴は、それぞれ「AND」と「OR」の範囲が逆転するという点です。
ちなみにこの2つも広い括りでは論理演算子として扱われることもあるみたいです。
NAND (論理否定積)
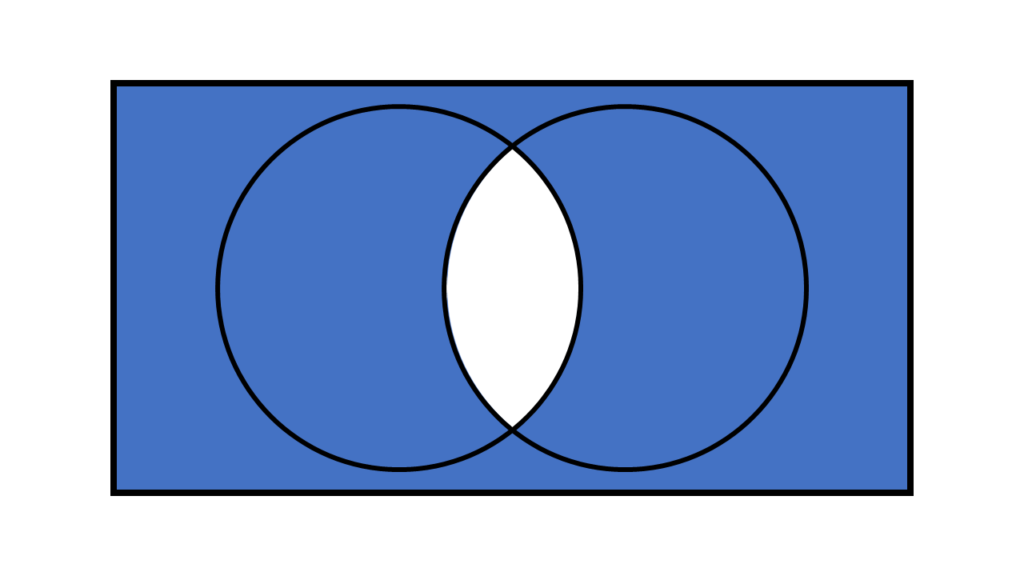
NANDはANDの範囲を逆転したものです。
(ANDとNOTの組み合わせ)
2つの条件両方を満たすものを偽、それ以外を真とします。
NOR (論理否定和)
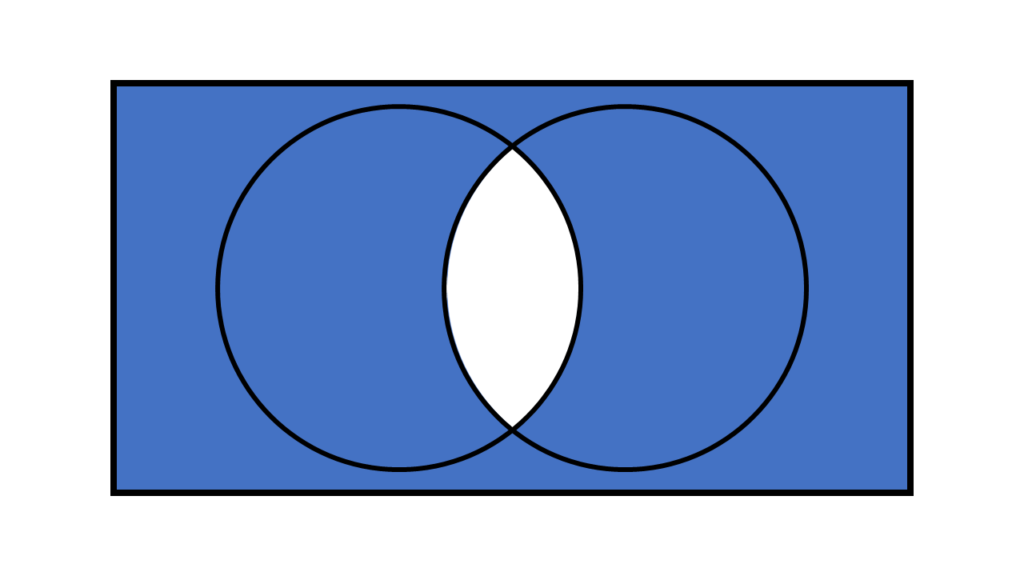
NORはORの範囲を逆転したものです。
(ORとNOTの組み合わせ)
いずれか一方でも条件を満たすものを偽、それ以外を真とします。
まとめ
簡単な説明でしたが、論理演算についてざっくりは理解していただけたでしょうか?
ハンドコードのプログラミングはもちろん、回路やMBD(モデルベース開発)などでも同じ考えを使うので意外と関わる人も多いと思います。
私も昔「NAND」と「NOR」がいつもあいまいになって、ことあるごとにネットで調べてました。
最初はめんどくさいかもしれませんが、ぜひ慣れていってください。