必要条件と十分条件ってどっちがどっち??【理系雑学】
「必要条件」「十分条件」
本などにも使われている表現なので、理系の方でなくても見かける機会はあるのではないでしょうか。
ではどっちがどっちの意味なのか覚えてますか?
(そもそもどっちも意味を知らいよ!って方もいると思います。)
私は正直結構混ざるので、ちょっと整理のためもかねて記事にしてみました。
必要条件と十分条件とは
まずは定義の確認をしていきましょう。
2つの条件pとqにおいて、「pならばq」が成り立つとき
・qはpの必要条件
・pはqの十分条件
と言います。
はい、これが定義です。ピンときましたか?
現役理系学生の方なら問題ないと思いますが、私的にはこれでは理解が難しかったのでもう少しかみ砕いてみます。
必要条件 (q) とは、ある事柄が成り立つために必ず必要な条件です。
ただ必要条件を満たしてもある事柄が成り立たない場合もあります。
ある事柄を成り立たせるためには他の条件も一緒に満たさないといけない場合もあるからです。
十分条件 (p) とは、この条件を満たしたら必ずある事柄が成り立つ条件です。
言い換えればある事柄が成り立つにはこの条件を満たすだけで十分という条件のことです。
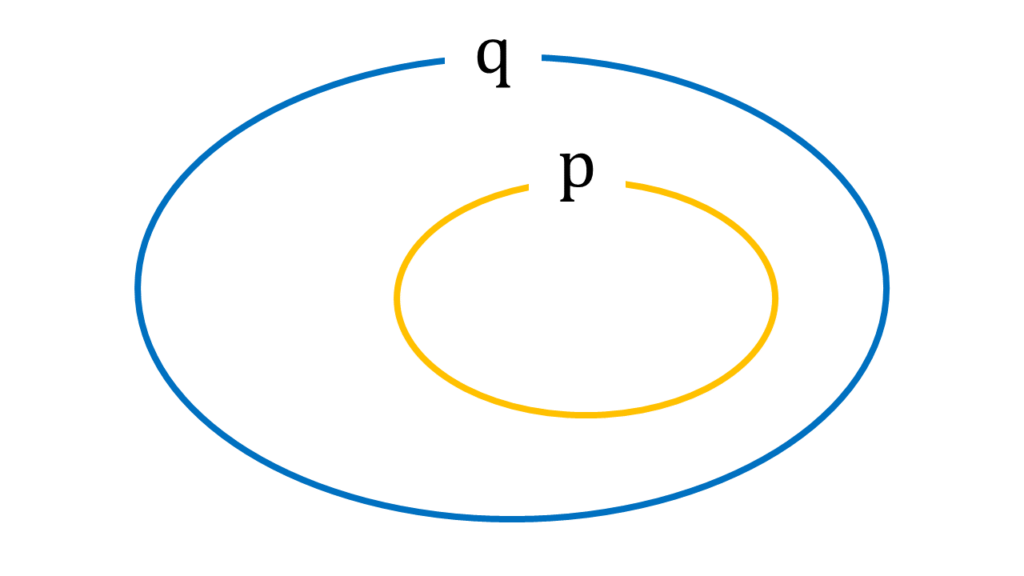
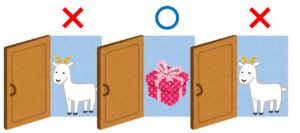
イメージで言うとこんな感じです。
pであれば必ずqになりますが、qでもpにならないところがあります。
必要条件と十分条件の例
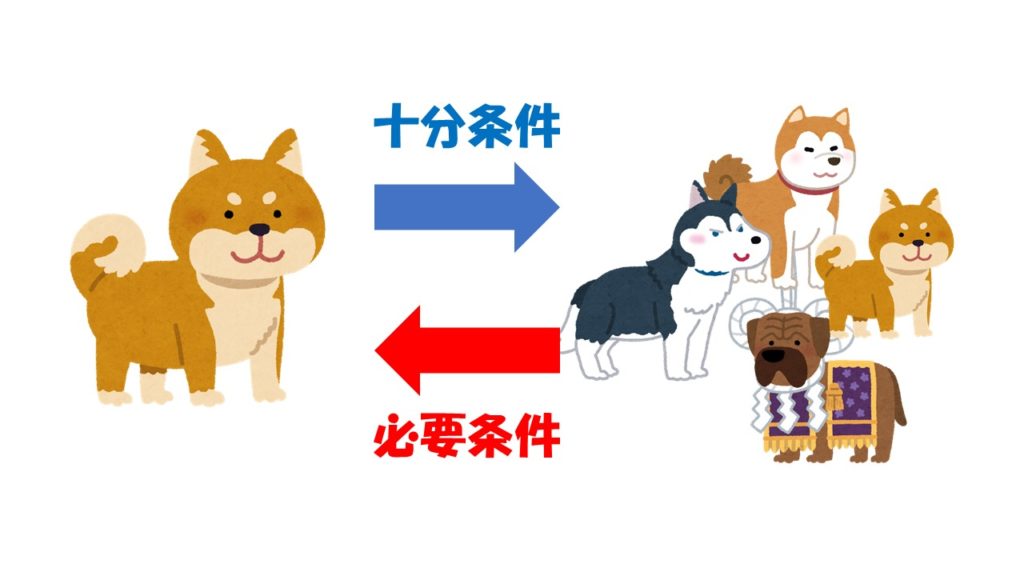
例えば犬と柴犬で考えてみましょう。
「柴犬ならば犬」
この命題は成り立ちます。このとき
・「犬」は「柴犬」の必要条件
・「柴犬」は「犬」の十分条件
となります。
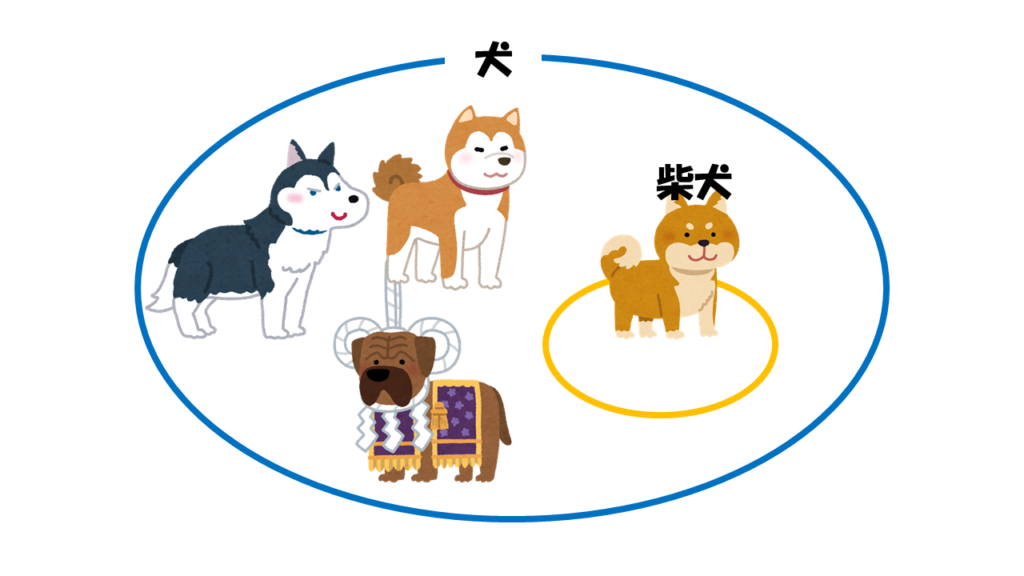
犬と言ってもシベリアンハスキーや秋田犬など、柴犬以外の可能性もあります。そのため柴犬には犬は必要な条件ではありますが、それだけでは柴犬だとは言い切れません。
そのため「犬は柴犬の十分条件」になります。
いっぽう、柴犬であれば必ず犬なので「柴犬は犬の十分条件」です。
必要十分条件
先ほどまでの必要条件と十分条件と似たようなものとして、「必要十分条件」というものがあります。
これは「pならばq」と「qならばp」のどちらも成り立つとき
・pはqの必要十分条件
・qはpの必要十分条件
と言います。
どんなときにこれが成り立つかイメージつきますか?
実はこれは「pとqが同じ(同値)」場合に起こります。
数学では出てきますが、単に同じ条件を比べているということなので、言葉としては普段使いしないですね。
まとめ
必要条件、十分条件の違いについて理解していただけたでしょうか?
もし覚えるとしたら
・「必要条件」はあることが成り立つために必ず必要な条件
・「十分条件」はあることが成り立つにその条件を満たすだけで十分な条件
と覚えると覚えやすいかもしれません。
ややこしいですが、ちょっとでも覚えやすかったり理解の足しにしていただけたら嬉しいです。